
Notice that this means the amount of interest earned after three years is $126.83. Round the number to the nearest cent (hundredth). The money you will have after 3 years will be A.įirst identify which of A, P, r, m, and t is being asked for, then determine values for the remaining variables.Ĭompounded quarterly means 4 times a year. If you invest $1,000 in an account paying 4% interest, compounded quarterly, how much money will you have after 3 years? A larger base also makes the graph closer to the y-axis for x > 0 and closer to the x-axis for x < 0. Notice that a larger base makes the graph steeper. The functions f( x) = 2 x, f(x) = 3 x, and Let’s compare the three graphs you’ve seen. X - axis, and gets steeper and steeper on the right. Use the shape of an exponential graph to help you: this graph gets very close to the x-axis on the left, but never really touches the
#Exponential graph series
The point is the blue point on this graph.įor other bases, you might need to use a calculator to help you find the function value.Ĭonnect the points as best you can, using a smooth curve (not a series of straight lines). Because you know the square root of 4, you can find that value in this case. You could also try other points, such as when x =. You can change the scale, but then our other values are very close together. Even with x as small as 2, the function value is too large for the axis scale you used before. Notice that the larger base in this problem made the function value skyrocket. If you think of f( x) as y, each row forms an ordered pair that you can plot on a coordinate grid. You can choose different values, but once again, it’s helpful to include 0, some positive values, and some negative values. This shows that all of the points on the curve are part of this function. Connect the points as best you can to make a smooth curve (not a series of straight lines).
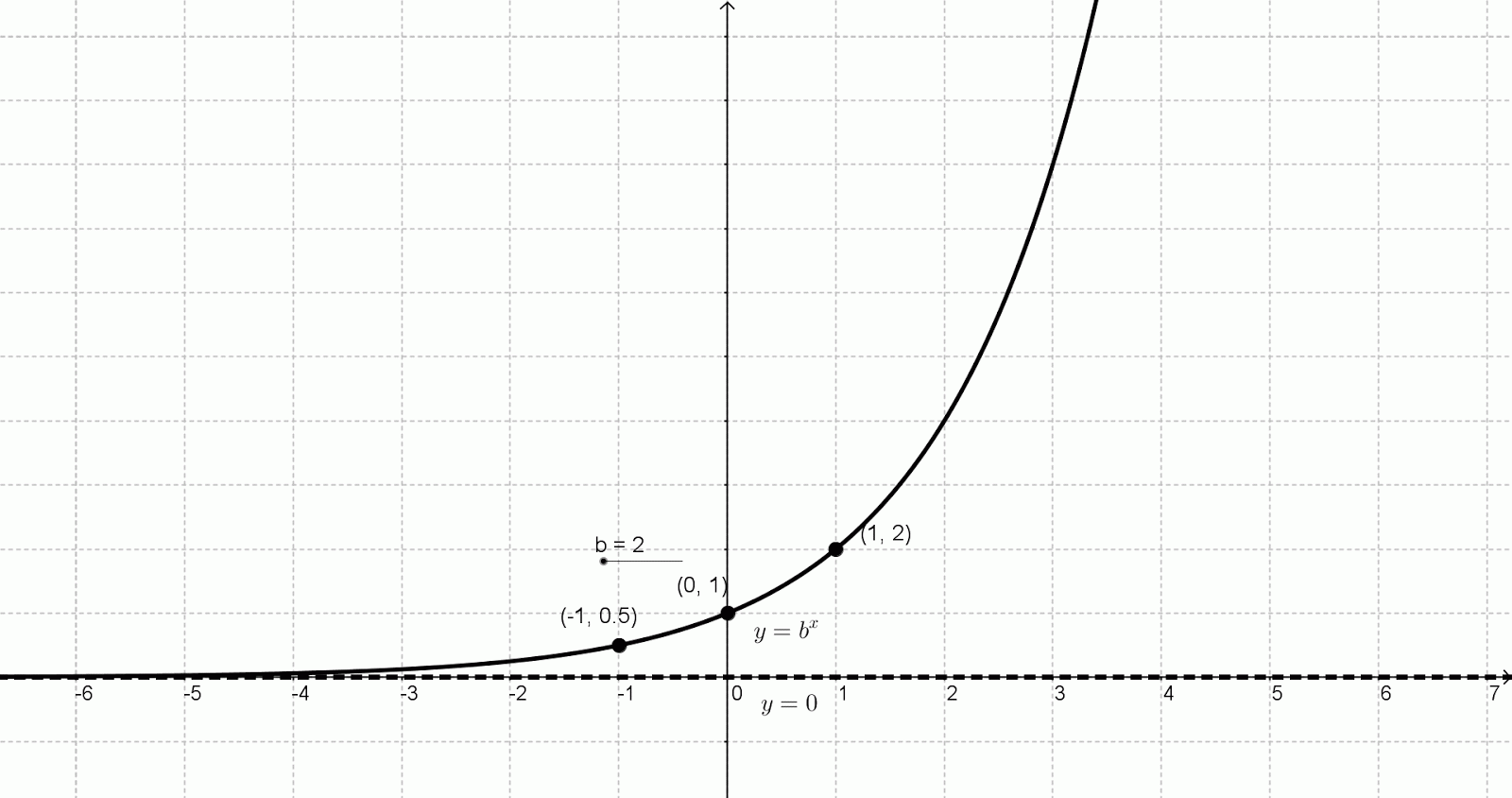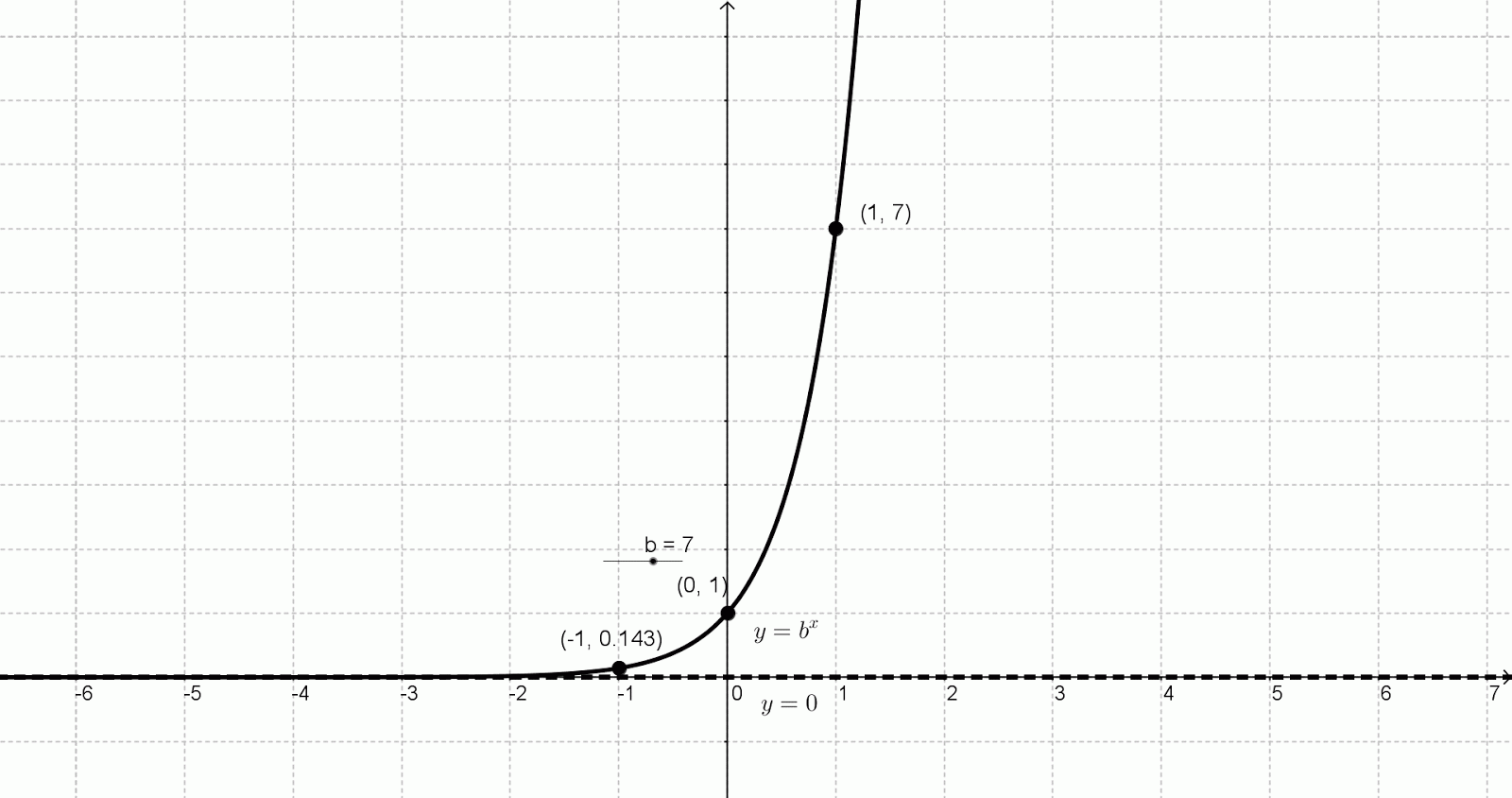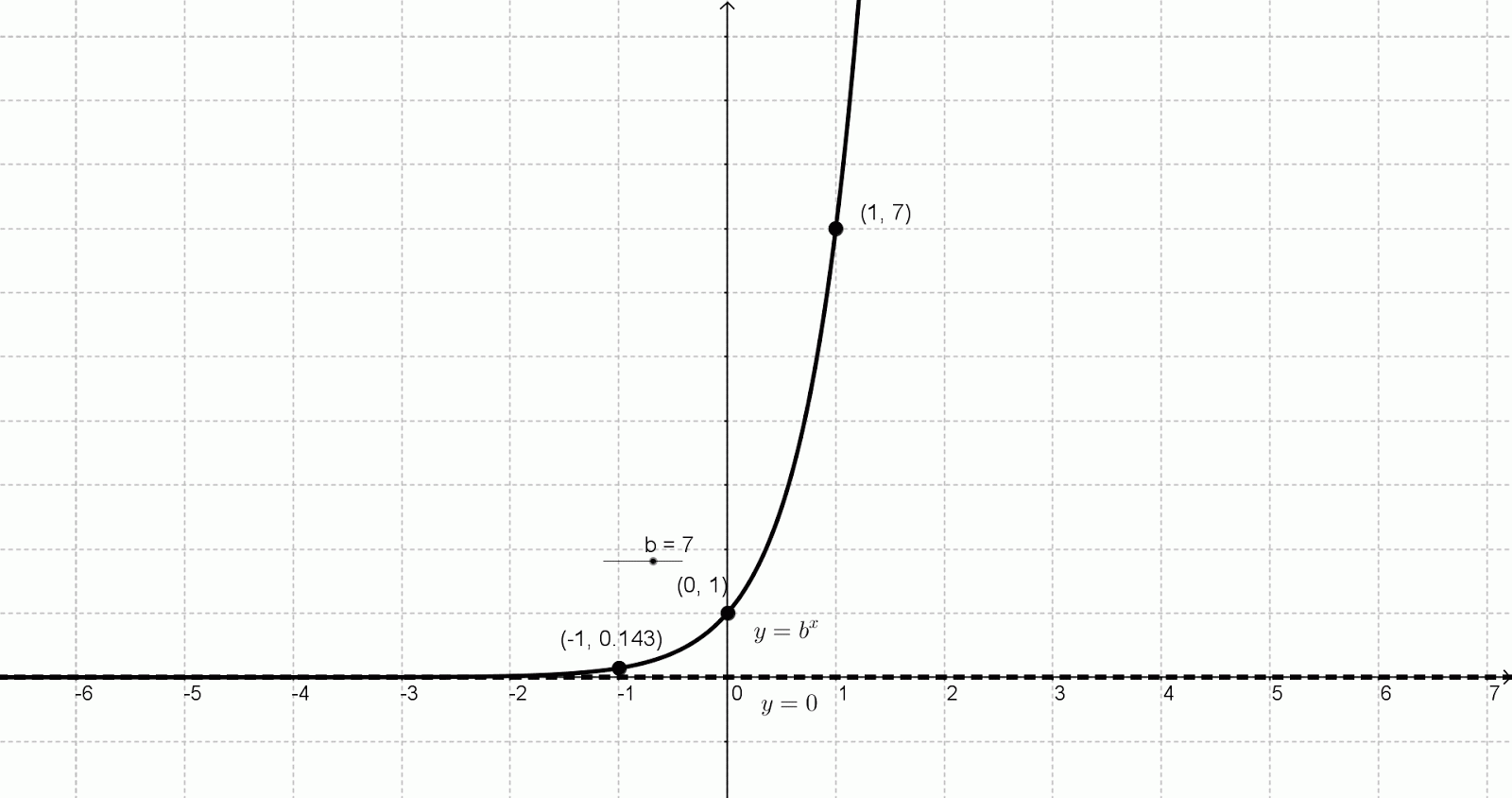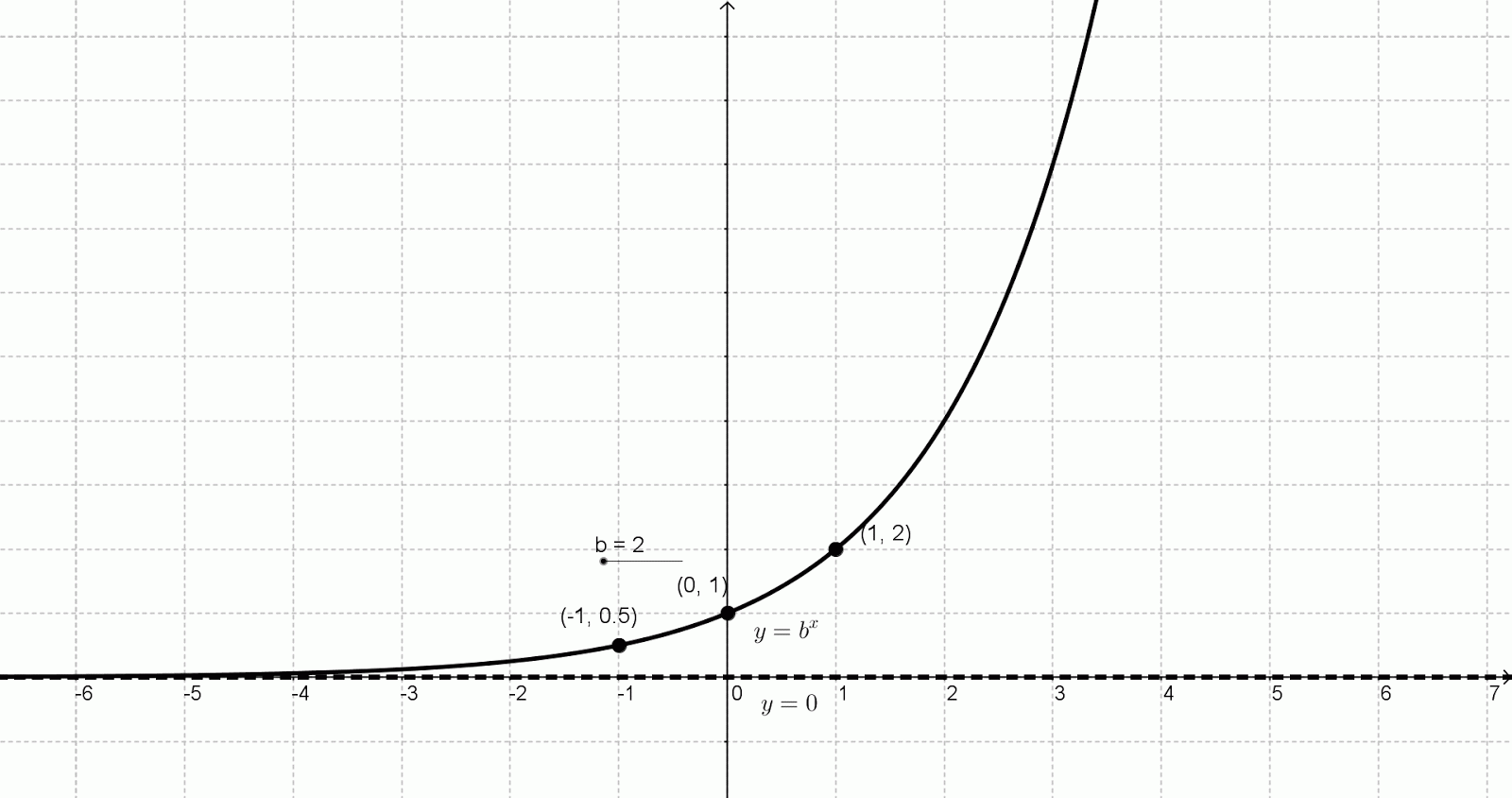
Now that you have a table of values, you can use these values to help you draw both the shape and location of the function. Think about what happens as the x values increase-so do the function values ( f( x) or y)! Note that your table of values may be different from someone else’s, if you chose different numbers for x. f(1) = 3 1 = 3, so 3 goes in the f( x) column next to 1 in the x column. X = −2, f( x) = 3 -2 =, so goes in the f( x) column next to −2 in the x column. Tip: It’s always good to include 0, positive values, and negative values, if you can.Įvaluate the function for each value of x, and write the result in the f( x) column next to the x value you used. Label the columns x and f( x).Ĭhoose several values for x and put them as separate rows in the x column. In this situation, you will need to examine the graph carefully to determine what is happening.Make a “T” to start the table with two columns. The horizontal shift will affect the y-intercept and the vertical shift will affect the possibility of an x-intercept. If the transformed parent function includes a vertical or horizontal shift, all bets are off. Like the parent function, this transformation will be asymptotic to the x-axis, and will have no x-intercept. Note that the value of a may be positive or negative. Again, algebraically speaking, when x = 0, we have y = ab 0 which is always equal to a The transformed parent function of the form y = ab x, will always have a y -intercept of a, occurring at the ordered pair of (0, a).There is no x-intercept with the parent function since it is asymptotic to the x-axis (approaches the x-axis but does not touch or cross it).
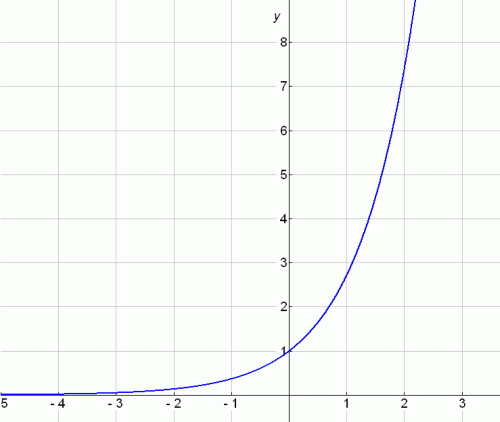
Algebraically speaking, when x = 0, we have y = b 0 which is always equal to 1. The parent function, y = b x, will always have a y -intercept of one, occurring at the ordered pair of (0,1).By examining the nature of the exponential graph, we have seen that the parent function will stay above the x-axis, unless acted upon by a transformation.


 0 kommentar(er)
0 kommentar(er)
